八皇后问题
经典八皇后问题(其实书中是N皇后)。要求求出N*N矩阵中,横竖斜只能存在一子的摆放方式的数量。
#include<iostream>
#include<cmath>
using namespace std;
const int maxn = 11;
int n,count,P[maxn],hashTable[maxn]={false};
void generateP(int index){
if(index==n+1){
count++;
return;
}
for(int x=1;x<=n;x++){
if(!hashTable[x]){
bool flag = true;
for(int pre=1;pre<index;pre++){
if(abs(index-pre)==abs(x-P[pre])){
flag=false;
break;
}
}
if(flag){
P[index]=x;
hashTable[x]=true;
generateP(index+1);
hashTable[x]=false;
}
}
}
}
int main(){
n=8;
generateP(1);
printf("%d",count);
return 0;
}
符号三角形
输入n为如下图三角形第一行长度,求可形成的+与-数量相同的三角形的数量。
其中同号在下一行中为+,异号在下一行中为-。
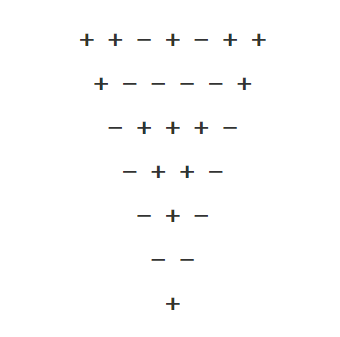
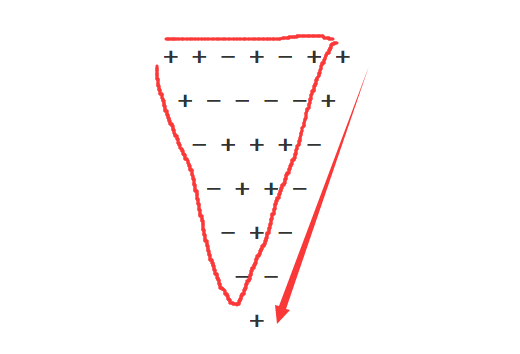
思路与八皇后十分相似。 第一行中每在末尾增加一位,无论正负都根据子三角形的最右侧一斜生成新三角形。即Triangle(n+1)=Triangle(n)+ObliqueLine(n+1)
每增加一位,就在前一位的三角形基础上进行运算和递归,后进行还原。
#include <stdio.h>
int sum,count;
int half;
int **p;
int n;
void backtrack(int t)
{
if((count>half)||(t*(t-1)/2-count>half)){
return;
}
if(t>n) {
sum++;
}else{
for(int i=0;i<2;i++)
{
p[1][t]=i;
count=count+i;
for(int j=2;j<=t;j++)
{
p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
count+=p[j][t-j+1];
}
backtrack(t+1);
for(int j=2;j<=t;j++){
count-=p[j][t-j+1];
}
count-=i;
}
}
}
int main()
{
printf("input the number of symbols in the first line:");
scanf("%d",&n);
count=0;
sum=0;
half=(n+1)*n/4;
if(n==1||n==2)
{
printf("Result:0");
return 0;
}
p=new int *[n+1];
for(int i=0;i<n+1;i++)
p[i]=new int[n+1];
for(int i=0;i<n+1;i++){
for(int j=0;j<n+1;j++){
p[i][j]=0;
}
}
backtrack(1);
printf("Result:%d.\n",sum);
return 0;
}